One SM gauge singlet scalar for seesaw and the inflaton? Ask the B-L Higgs!

An (ad hoc?) non minimal B-L Higgs inflation scenario at tree-level

Today I propose to carry on the cosmological inflation thema already addressed in the former post but forgetting about the dark matter issue - which is a tricky astrophysical puzzle - and focusing on the role the inflaton could also play in particle physics at very high energy.

Current understanding about the origin of our universe is that, for a very brief moment at the beginning, our universe went through a period of rapid accelerated expansion known as inflation. Inflation scenario [1, 2, 3, 4] was originally proposed to solve serious problems in the Standard Big-Bang Cosmology, namely, the horizon, flatness and monopole problems. In addition and more importantly in the view point of the current cosmological observations, inflation provides a mechanism to create primordial density fluctuations of the early universe which seed the formation of large scale structure of the universe that we see today. In a simple inflation scenario, inflation is driven by a single scalar field (inflaton) that slowly rolls down to its potential minimum (slow-roll inflation). During the slow-roll era, the inflaton energy is dominated by a slowly varying potential, which causes the universe to undergo a phase of an accelerated expansion. Quantum fluctuations of the inflaton field are stretched to macroscopic scales by inflation to yield the primordial density fluctuations. After inflation, the inflaton decays to the Standard Model (SM) particles and the decay products heat up the universe (reheating). The success of big bang nucleosynthesis scenario requires the reheating temperature to be TR >1 MeV. 

Recently the Planck 2015 results [5] have set an upper bound on the tensor-to-scalar ratio as r<0.11 while the best fit value for the spectral index (ns) is 0.9655 ± 0.0062 at 68% CL. Hence, the simple chaotic inflationary scenario with the inflaton potentials V∝φ⁴ and V∝φ² are disfavored because their predictions for r are too large. Among many inflation models, λφ⁴ inflation with non-minimal gravitational coupling (ξφ²R, where φ is inflaton, R is the scalar curvature, and ξ is a dimensionless coupling) is a very simple model, which can satisfy the constraints by the Planck 2015 with ξ > 0.001 [6].

Given that we need interactions between SM particles and inflaton for a successful reheating of the universe, a more compelling inflation scenario would be where the inflaton field plays another important role in particle physics. As an example of such a scenario, we may consider the (general) Higgs model, where a scalar (Higgs) field plays the crucial role to spontaneously break the gauge symmetry of the model, and we identify the Higgs field as inflation. The SM Higgs inflation [7, 8, 9] is nothing but this scenario, where the SM Higgs boson plays the role of inflaton with non-minimal gravitational coupling. Because of the observed Higgs boson mass of around 125 GeV, the SM Higgs effective potential is likely unstable. If this is the case, the original SM Higgs inflation cannot work any more, and some extension is necessary [12]. However, we may apply the same idea to the general Higgs model and identify the Higgs field of the model (not the SM Higgs field) as inflaton in the presence of non-minimal gravitational coupling. For a simple example, see [18]...

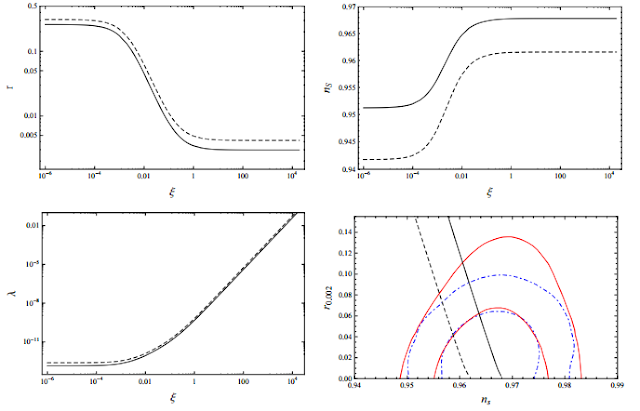
Fig. 1 shows inflationary predictions for the non-minimal λφ⁴ inflation at the tree-level for N = 50 (dashed-dotted) and N=60 (solid). Top panels show r vs. ξ (left) and ns vs. ξ (right). Both r and ns show asymptotic behavior for both small and large ξ values. In the minimal λφ⁴ inflation limit with ξ=0, we obtain r≃0.31 (0.26) and ns≃0.942 (0.951) for N = 50 (60). The plots also show that for a larger e-holding number, we obtain a larger ns while a smaller r. The bottom-left panel shows the tree level quartic coupling λ as a function of ξ. Note that λ is very small unless ξ ≫ 1. The inflationary predictions for ns and r for various values of ξ are depicted in the bottom-right panel along with the results from the measurements by Planck 2015 and Planck+BICEP2/Keck Array [5]. We see that the inflationary predictions for ξ >0.001 are consistent with the observations. 

Running Non-Minimal Inflation with Stabilized Inflaton Potential

Nobuchika Okada, Digesh Raut

(Submitted on 15 Sep 2015 (v1), last revised 22 Sep 2015 (this version, v2))

Taking into account quantum corrections?

We have considered the general Higgs model with the gauge and Yukawa interactions with the spontaneous gauge symmetry breaking. In the presence of the non-minimal gravitational coupling, the Higgs field can also play the role of inflaton. The analysis with the Higgs potential at the tree-level leads to the inflationary predictions consistent with the cosmological observations. However, once we take quantum corrections, the effective inflaton potential most likely becomes unstable. This is because the inflaton quartic coupling is extremely small in a large portion of the parameters space and the effective potential is controlled by the gauge and Yukawa couplings independently of the quartic coupling. In the renormalization group improved effective potential, we see that the running quartic coupling becomes negative in the vicinity of the initial inflaton value, indicating the instability of the effective potential. In order to avoid this problem, we have imposed the stability condition of vanishing the beta function of the inflation quartic coupling. This condition leads to a non-trivial relation between the gauge and fermion masses. Since the renormalization group evolution of the inflaton quartic coupling is mainly controlled by the gauge and Yukawa coupling, the inflation mass at low energy is determined by the couplings. Therefore, the mass spectrum of the gauge boson, fermion and inflation shows a non-trivial relation.

Since the inflaton potential is modified from the tree-level one, the inflationary predictions are altered from those obtained by the tree-level analysis. Although the prediction of the tensor-to-scalar ratio remains the same under the condition of the vanishing beta function, the predictions for the scalar spectral index and the running of the spectral index can be significantly altered. The fact that the effective potential is controlled by the gauge and Yukawa couplings implies a correlation between the inflationary predictions and the particle mass spectrum. Therefore, the observables at the gauge symmetry breaking scale correlate with the inflationary predictions which determined by physics at an extremely high energy compared to the gauge symmetry breaking scale.  

By taking the minimal B − L extension of the Standard Model as a simple example, we have shown such a non-trivial relation in the particle mass spectrum driven by the stability condition of the effective inflaton potential. We also have calculated the inflationary predictions from the effective potential and found their dependence of the B−L gauge coupling. Therefore, the new particle mass spectrum of the B − L model, once observed, has an implication to the inflationary predictions. On the other hand, more precise measurements of the inflationary predictions yield a constraint on the B − L particle mass spectrum... 

Id. 

or waiting for a natural embedding in a spectral extension of the standard model?

... we found a reformulation of noncommutative geometry (NCG) that simplified and unified the mathematical axioms while, at the same time, resolving a problem with the NCG construction of the standard model Lagrangian, by precisely eliminating 7 terms which had previously been problematic. In this paper, we show that this same reformulation leads to a new perspective on the gauge symmetries associated to a given NCG, uncovering some that were previously missed. In particular, when we apply our formalism to the NCG traditionally used to describe the standard model of particle physics, we find a new U(1)B−L gauge symmetry (and, correspondingly, a new B − L gauge boson). This, in turn, implies the existence of a new complex Higgs field σ that is a singlet under SU(3)C×SU(2)L×U(1)Y but transforms with charge +2 under U(1)B−L, allowing it to form a majorana-like Yukawa coupling σνRνR with two right-handed neutrinos (so that, if it obtains a large VEV, it induces seesaw masses for the neutrinos). It is striking, on the one hand, that this precise extension of the standard model has been previously considered in the literature [22, 23] on the basis of its cosmological advantages; and, on the other hand, that the new field σ can resolve a previous discrepancy between the observed Higgs mass and the NCG prediction [18–21]... It is important to carefully reconsider the phenomenological and cosmological implications of the standard model extension which we have landed on here, especially in light of the extra constraints imposed by the spectral action. This is an exciting topic for future work.

Rethinking Connes' approach to the standard model of particle physics via non-commutative geometry

Shane Farnsworth, Latham Boyle

(Submitted on 22 Aug 2014 (v1), last revised 14 Jan 2015 (this version, v2))