One SM gauge singlet scalar for a non-minimal quartic or quadratic inflaton? Ask COrE+, PIXIE and LiteBIRD!

//This post has been updated and some figures corrected on 10 November 2015

Is an inflaton non-minimally coupled with gravity the simplest inflation model compatible with experiment?

... we briefly review and update the results of five closely related, well motivated and previously studied inflationary models which are consistent with values of the tensor to scalar ratio r around 0.05, a signal level which will soon be probed. The first two models employ the very well known quadratic (φ²) and quartic (φ⁴) potentials [5], supplemented in our case by additional couplings of the inflaton φ to fermions and/or scalars {such as (1/2)hφNN or (1/2)g²φ²χ² to a Majorana fermion N and a scalar χ respectively}, so that reheating becomes possible. These new interactions have previously been shown [6, 7, 8] to significantly modify the predictions for the scalar spectral index n_s and r in the absence of these new interactions. The next two models exploit respectively the Higgs potential [7–11] and Coleman-Weinberg potential [10, 12, 13, 14]. With the SM electroweak symmetry presumably broken by a Higgs potential, it seems natural to think that nature may have utilized the latter (or the closely related Coleman-Weinberg potential) to also implement inflation, albeit with a SM singlet scalar field. Finally, we consider a class of models [15, 16] which invokes a quartic potential for the inflaton field, supplemented by an additional non-minimal coupling of the inflaton field to gravity [8, 17]. Our results show that the predictions for n_s and r from these models are generally in good agreement with the BICEP2, Planck and WMAP9 measurements, except the radiatively corrected quartic potential which is ruled out by the current data. We display the range of r values allowed in these models that are consistent with n_s being close to 0.96. Finally, we present the predictions for {the running of the scalar spectral index α=|dn_s/dlnk|} which turn out to be of order 10^-4-10^-3.

Radiatively corrected φ² potential:  

n_s vs. r (left panel) and n_s vs. α (right panel) for various κ∝(2h⁴ − g⁴) values, along with the n_s vs. r contours (at the confidence levels of 68% and 95%) given by the Planck collaboration (Planck TT+lowP) [3]. The black points and triangles are predictions in the textbook quartic and quadratic potential models, respectively. The dashed portions are for κ<0 {with suppressed r for larger |κ|. The number of e-folding} is taken as 50 (left curves) and 60 (right curves). {blogger's comment: the  r=0.028 value indicated by the cross and the smallest n_s vs. r contour are updates thanks to BICEP2/Keck data through the end of the 2014 season including new 95 GHz maps [arxiv.org/abs/1510.09217]}

Radiatively corrected φ⁴ potential:...

Higgs potential:

...The dashed portions are for the initial inflaton VEV larger than its VEV at the potential minimum. 

Coleman-Weinberg potential: 

...The dashed portions are for the initial inflaton VEV larger than its VEV at the potential minimum.

φ⁴ potential with non-minimal gravitational coupling: 

... for various ξ values along each curve from 0 (top left) to ξ≫1 (down right)

The Observational Status of Simple Inflationary Models: an Update

Nobuchika Okada, Vedat Nefer Şenoğuz, Qaisar Shafi

(Submitted on 25 Mar 2014 (v1), last revised 13 May 2015 (this version, v4))

Getting the mass of a Big broson from a testable inflation model? 

... the first attempts to make a joint analysis of Planck and BICEP2 data have been presented [11, 13] concluding that the quadratic chaotic inflation (CI) is disfavored at more than 95% confidence level... it was shown several years ago [14] that a quadratic (or quartic) potential can, at best, function as an approximation within a more realistic inflationary cosmology. The end of CI is followed by a reheating phase which is implemented through couplings involving the inflaton and some additional suitably selected fields. The presence of these additional couplings can significantly modify, through radiative corrections (RCs), the tree level inflationary potential. For instance, for a quadratic potential supplemented by a coupling of the inflation field to, say, right-handed neutrinos, r can be reduced to values close to 0.05 [5] or so, at the cost of a (less efficient) reduction of ns , though. In this paper we briefly review this idea taking into account the recent refinements of Ref. [15], according to which an unavoidable dependence of the results on the renormalization scale arises. 

Another mechanism for reducing r at an acceptable level within models of quadratic CI is the introduction of a strong, linear non-minimal coupling of the inflaton to gravity [16,17]. The aforementioned mechanism, that we mainly pursue here, can be applied either within a supersymmetric (SUSY) [16] or a non-SUSY [17] framework. The resulting inflationary scenario, named non-minimal CI (nMI), belongs to a class of universal “attractor” models [18], in which an appropriate choice of the non-minimal coupling to gravity suitably flattens the inflationary potential, such that r is heavily reduced but ns stays close to the currently preferred value of 0.96. 

In this work we reexamine the realization of nMI based on the quadratic potential implementing the following improvements:

• As regards the non-SUSY case, we also consider RCs to the tree-level potential which arise due to Yukawa interactions of the inflaton – cf. Ref. [20, 21]. We show that the presence of RCs can affect the ns values of nMI – in contrast to minimal CI, where RCs influence both ns and r. For subplanckian values of the inflaton field, though, r remains well suppressed and may be observable only in the next generation of experiments such as COrE+ [22], PIXIE [23] and LiteBIRD [24] which may bring the sensitivity down to 10^-3. [For ns = 0.96 the model favors fermionic coupling of the inflaton with strength in the range (0.01−3.5) and predicts r≃0.003 and inflaton mass m≃ 3·10¹³GeV.] 

• As regards the SUSY case, following Ref. [25], we generalize the embedding of the model in SUGRA allowing for a variation of the numerical prefactor encountered in the adopted Kähler potential... 

We finally show that, in both of the above cases, the ultaviolet (UV) cut-off scale [28, 29] of the theory can be identified with the Planck scale and, thus, concerns regarding the naturalness of this kind of nMI can be safely evaded. It is worth emphasizing that this nice feature of these models was recently noticed in Ref. [30] and was not recognized in the original papers [16, 17].

Gravity Waves From Non-Minimal Quadratic Inflation

Constantinos Pallis, Qaisar Shafi

(Submitted on 11 Dec 2014 (v1), last revised 27 Mar 2015 (this version, v3))

 Let us wait for future cosmological probes

The value of the tensor-to-scalar ratio r in the region allowed by the latest Planck 2015 measurements can be associated to a large variety of inflationary models. We discuss here the potential of future Cosmic Microwave Background cosmological observations in disentangling among the possible theoretical scenarios allowed by our analyses of current Planck temperature and polarization data. Rather than focusing only on r, we focus as well on the running of the primordial power spectrum, α_s and the running of thereof, β_s. Our Fisher matrix method benefits from a detailed and realistic appraisal of the expected foregrounds. Future cosmological probes, as the COrE mission, may be able to reach an unprecedented accuracy in the extraction of βs and rule out the most favoured inflationary models... 

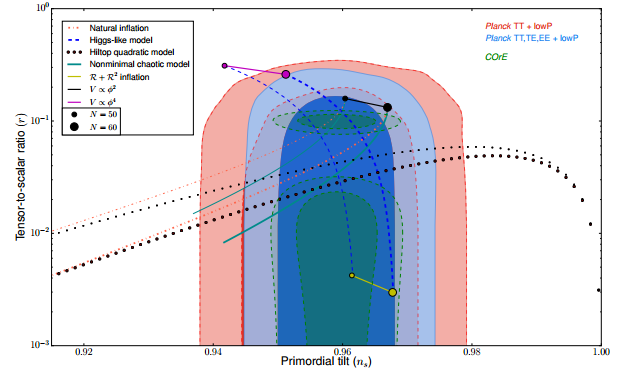
Notice, from the {figure above}, that the trajectories in the (n_s, r) plane for the non-minimally coupled case (ξRφ²) start always at the point corresponding to the φ² model predictions, and then, as the coupling ξ takes positive values, the tensor contribution is reduced, and the scalar spectral index ns is pushed below scale invariance, see Ref. [24].

The present and future of the most favoured inflationary models after Planck 2015

Miguel Escudero, Héctor Ramírez, Lotfi Boubekeur, Elena Giusarma, Olga Mena

(Submitted on 17 Sep 2015)

The first model of inflation, proposed by Starobinsky [1], is based on a conformal anomaly in quantum gravity. The Lagrangian density f(R) = R+R²/(6M²), where R is a Ricci scalar and M is a mass scale of the order of 10¹³GeV, can lead to a sufficient amount of inflation with a successful reheating [7]. Moreover, the Starobinsky model is favored from the 1-st year Planck observations [6]. The “old inflation” [2], which is based on the theory of supercooling during the cosmological phase transition, turned out to be unviable, because the Universe becomes inhomogeneous as a result of the bubble collision after inflation. The revised version dubbed “new inflation” [8, 9], where the second-order transition to true vacuum is responsible for cosmic acceleration, is plagued by a fine-tuning problem for spending enough time in false vacuum. However, these pioneering ideas opened up a new paradigm for the construction of workable inflationary models based on theories beyond the Standard Model of particle physics (see e.g., Refs. [10–13]). Most of the inflationary models, including chaotic inflation [14], are based on a slow-rolling scalar field with a sufficiently flat potential. One can discriminate between a host of inflaton potentials by comparing theoretical predictions of the scalar spectral index ns and the tensor-to-scalar ratio r with the CMB temperature anisotropies (see, e.g., [15–18])...

In Starobinsky inflation the scalar spectral index and the tensor-to-scalar ratio are given by ns=1−2/N and r=12/N² respectively, in which case the model is well within the 68 % CL region. In Higgs inflation, described by the potential V(φ)= λ₄/4(φ²−v²)² (v∼10²GeV), the presence of non-minimal couplings −ξφ²R/2 with |ξ|≫1 gives rise to the Einstein-frame potential similar to that in Starobinsky inflation, so that ns and r are the same in both models as long as quantum corrections to the tree-level Higgs potential are suppressed. It is possible to realize the self coupling λ₄ of the order of 0.1 at the expense of having a large negative non-minimal coupling ξ∼−10⁴... 

It is expected that future observations of CMB polarization such as LiteBIRD will provide further tight constraints on the amplitude of gravitational waves. We hope that we can approach the best model of inflation in the foreseeable future.

Distinguishing between inflationary models from cosmic microwave background

Shinji Tsujikawa

(Submitted on 19 Jan 2014 (v1), last revised 12 Jun 2014 (this version, v2))