Three caravels to sail towards the Cape of Grand Unification

The blogger is back and begins his first exploration of "spectral models" as announced just before his departure on holidays on July 19! 

Travelling light to go far enough

The very last post was about an interesting achievement by Babu and Khan consisting in the building of a minimal non-supersymmetric grand unification model with a Pati-Salam intermediate scale following the programmatic extension of the Standard Model in the orthodox line of quantum Yang-Mills-Higgs fields theory.  I have found this work interesting for different reasons, the most important one for today's post being it has freed from the burden of the pre-LHC ideology of the naturalness problem regarding the Higgs scalar (these days there is a more expert blogger raising this issue).

The naturalness principle strongly influenced high-energy physics in the past decades [1], leading to the belief that physics beyond the Standard Model (SM) must exist at a scale ΛNP such that quadratically divergent quantum corrections to the Higgs squared mass are made finite (presumably up to a log divergence) and not much larger than the Higgs mass Mh itself. This ideology started to conflict with data after TeVatron measured the top mass (which implies a sizeable order-one top Yukawa coupling λt) and after LEP excluded new charged particles below 100 GeV [2]...  

The most plausible new physics motivated by naturalness is supersymmetry. It adds new particles at the weak scale, with the lightest one possibly being Dark Matter (DM). Further support for this scenario come from gauge unification and from the fact that DM loosely around the weak scale is indicated by the hypothesis that DM is the thermal relic of a massive stable particle. Doubting that nature is natural seemed impossible. However, no new physics has been so far seen at LHC with √s=8TeV... While this is not conclusive evidence, while special models that minimise fine-tuning are being considered, while naturalness arguments can be weakened by allowing for a finer tuning, while various searches have not yet been performed, while LHC will run at higher energy, etc, it is fair to say that the most straightforward interpretation of present data is that the naturalness ideology is wrong.

A modified naturalness principle and its experimental tests

Marco Farina, Duccio Pappadopulo, Alessandro Strumia

(Submitted on 28 Mar 2013 (v1), last revised 29 Apr 2014 (this version, v3))

Skipping (for a while) naturalness requirements to progress in the understanding of physics at higher energy scale can sound hazardous but this is precisely the philosophy of this blog to follow a different shipping route...

Bringing gauge coupling running charts as modern Portolans

Let's report thus on the recently prepublished first proof of the Pati-Salam gauge couplings in the three spectral models compatible with the actual mathematical framework of noncommutative geometry and the physical principal of spectral action. We will comment afterwards on the common grounds and differences between these spectral models and the work of Babu and Khan.

This paper builds on ... recent discoveries in the noncommutative geometry approach to particle physics:... the original argument by classification [4] of finite geometries F that can provide the fine structure of Euclidean space-time as a product M×F (where M is a usual 4-dimensional Riemannian space) has now been replaced by a much stronger uniqueness statement [7, 8]. This new result shows that the algebra

 M2(H)⊕M4(C), (1) 

where H are the quaternions, appears uniquely when writing the higher analogue of the Heisenberg commutation relations. This analogue is written in terms of the basic ingredients of noncommutative geometry where one takes a spectral point of view, encoding geometry in terms of operators on a Hilbert space H. In this way, the inverse line element is an unbounded self-adjoint operator D. The operator D is the tensor sum of the usual Dirac operator on M and a ‘finite Dirac operator’ on F, which is simply a hermitian matrix D_F. The usual Dirac operator involves γ matrices which allow one to combine the momenta into a single operator. The higher analogue of the Heisenberg relations puts the spatial variables on similar footing by combining them into a single operator Y using another set of γ matrices and it is in this process that the algebra (1) appears canonically and uniquely in dimension 4. We refer to [7, 8] for a detailed account. What matters for the present paper is that the above process leads without arbitrariness to the Pati–Salam [19] gauge group SU(2)R×SU(2)L×SU(4), together with the corresponding gauge fields and a scalar sector, all derived as inner perturbations of D [9]. Note that the scalar sector can not be chosen freely, in contrast to the early work on Pati–Salam unification [1, 10, 12, 13]. In fact, there are only a few possibilities for the precise scalar content, depending on the assumptions made on the finite Dirac operator. 

From the spectral action principle, the dynamics and interactions are described by the spectral action [2, 3], 

tr(f(D_A/Λ)) (2) 

where Λ is a cutoff scale and f an even and positive function... This action is interpreted as an effective field theory for energies lower than Λ. 

One important feature of the spectral action is that it gives the usual Pati–Salam action with unification of the gauge couplings [9] ... This is very similar to the case of the spectral Standard Model [6] where there is unification of gauge couplings. Since it is well known that the SM gauge couplings do not meet exactly, it is crucial to investigate the running of the Pati–Salam gauge couplings beyond the Standard Model and to find a scale Λ where there is grand unification: 

g_R(Λ) = g_L(Λ) = g(Λ). (4) 

This would then be the scale at which the spectral action... is valid as an effective theory. There is a hierarchy of three energy scales: SM, an intermediate mass scale m_R where symmetry breaking occurs and which is related to the neutrino Majorana masses (10¹¹ − 10¹³Gev), and the GUT scale Λ.

For simplicity, we restrict our analysis to the running of the gauge couplings at one-loop. Indeed, at two loops, the gauge and scalar couplings are mixed and influence each other. Moreover, the running of the scalar mass terms can not be trusted at all because of quadratic divergences. 

... depending on the assumptions on D_F , one may vary to a limited extent the scalar particle content, consisting of either composite or fundamental scalar fields... 

This is a general prediction of the spectral construction that there is 16 fundamental Weyl fermions per family, 4 leptons and 12 quarks ...

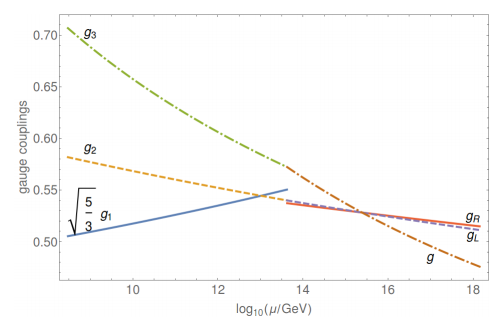
Running of coupling constants for the spectral Pati–Salam model with composite Higgs fields: g1, g2, g3 for µ < m_R and g_R, g_L, g for µ > m_R with unification scale Λ ≈ 2.5×10¹⁵ GeV for m_R=4.25×10¹³ GeV.

...

Running of coupling constants for the spectral Pati–Salam model with fundamental Higgs fields: g1, g2, g3 for  µ<m_R and g_R, g_L, g for µ > m_R with unification scale Λ ≈ 6.3×10¹⁶ GeV for m_R=1.5×10¹¹ GeV.

...

Running of coupling constants for the left-right symmetric spectral Pati–Salam model: g1, g2, g3 for µ < m_R and g_R, g_L, g for µ > m_R with unification scale Λ ≈ 2.7×10¹⁵ GeV for m_R=5.1×10¹³ GeV. 

...

We have analyzed the running of the Pati–Salam gauge couplings for the spectral model, considering different scalar field contents corresponding to the assumptions made on the finite Dirac operator. We stress that the number of possible models is quite restrictive and that one can not freely choose the particle content. We have identified the three main models, although there exists small variations on them. The different possibilities correspond to restrictions on the geometry of the finite space F. In all the models considered here, we establish unification of the gauge couplings, with boundary conditions set by the usual Standard Model gauge couplings at an intermediate mass scale. Besides the direct physical interest of such grand unification, it also determines the scale at which the asymptotic expansion of  [the spectral action] is actually valid as an effective theory.

Grand Unification in the Spectral Pati-Salam Model

Ali H. Chamseddine, Alain Connes, Walter D. van Suijlekom

(Submitted on 29 Jul 2015)

//Additional material (25 August 2015)
Would the spectral action grand unification thrill the heart of James Bjørken?
It might be interesting to stress that these spectral models enjoy grand unification gauge coupling without proton decay, the most famous prediction of grand unification theories from the past:

I remember an occasion, in 1974, when I was visiting SLAC. “Bj” Bjørken told me that he had recently read the article on SU(5) by Georgi and Glashow [99]. He said that, as he was reading it, his heart was pounding faster and faster at the beauty of the unification of QCD and the electroweak theory, the convincing explanation of the commensurate integer and fractional charges of quarks and leptons, etc., etc. But, Bj said, his heart sunk when he read that protons were not forever. At the time I thought his reaction was precisely the wrong one. Proton decay, I thought, was the best part of this Grand Unification: a candidate for the ultimate Yang-Mills (YM) theory, including such a fantastic prediction! With the benefit of thirty years of hindsight, I am beginning to wonder whether Bj was right... 

Grand unifications of YM theories and proton instability actually slightly preceded the work by Georgi and Glashow. Indeed, Jogesh Pati and Abdus Salam were the first to introduce the elegant idea of lepton number as a fourth colour [104]. I learned from Bram Pais, via Georgi [31], that their SU(2)⊗ SU(2)⊗ SU(4) group even contained the full SU(3)⊗SU(2)⊗U(1) gauge structure of the standard model! But they proceeded to break colour SU(3) into integrally-charged Han–Nambu quarks, thereby distantiating themselves from the current standard lore. The Harvard theorists were, this time, capable of immediately convincing experimentalists that proton decay was interesting to look for. Larry Sulak, in particular, was enthusiastic with the idea, and he was among those who developed the inverse-osmosis technique that proved to be crucial in making water —at a reasonable cost— sufficiently transparent to exploit a large water-Cerenkov detector. Larry ˇ deprived his colleagues at the University of Michigan of an elevator, to install in its shaft a sufficiently tall water container and test the technique. His colleagues may not have appreciated their extra stair-climbing efforts, but eventually this kind of detectors made great serendipitous discoveries: neutrinos from SN1987A, neutrino oscillations, ... Proton decay has not been observed to date, and who knows what future proton-decay detectors may uncover.

Fifty years of Yang-Mills Theories: a phenomenological point of view

Alvaro De Rujula

As one can read it, the proton decay hypothesis has not been confirmed but was a fantastic incentive to build better detectors making possible the neutrino oscillations detection, the only experimentally established physics beyond the Standard Model up to now!