A purported excess at 700 GeV for what kind of events at LHC2?

//last edition December 13 2015
A bump on a heavy diquark-invariant mass distribution for Higgsmas 2015 

The blogosphere has started to propagate a rumor about what physicists from CERN might talk about next week (see the former post). It's all about "a 750 GeV diphoton excess at >3σ, seen by both ATLAS and CMS" and "seems very hard to accommodate with the absence of such a bump in Run 1" to quote Jackson Clarke at Syymmetries. To celebrate Higgsmas 2015, I propose below another subject with slightly different premises (same energy range anomaly but in a very different channel) but which might have connection too with a potential future, who knows. Last but not least the authors of the following work propose an explanation for the absence of their hypothetical excess in LHC1 data so we can already learn some physics from the rumor eventually.  

At present the Standard Model (SM) successfully describes all experimental data in particle physics. Moreover, it is theoretically consistent and applicable up to the Planck scale, M_Pl ≈ 1.2×10¹⁹ GeV. On the other hand, there are many natural questions, which cannot be answered within the SM framework. For example, chiral anomalies are canceled only when quarks and leptons are considered simultaneously. At the same time these two sectors are completely independent within the SM. 

The hope that the different gauge coupling constants of the SU(3)_C×SU(2)_W×U(1)_Y  SM group meet at a single unification point has failed [1]. Therefore, if we, nevertheless, expect such unification, new physics should be introduced at some scale above the electroweak unification. In this paper we will consider the one-loop approximation to the gauge coupling evolution modifying only the Higgs sector of the SM. The matter sector of the SM consists of electroweak doublets: fermionic and bosonic ones. The SM contains only one bosonic doublet of the Higgs fields. We will assume that the number of the bosonic doublets N above some scale could be greater than one, while the number of the fermionic doublets is not modified. At present there are practically no limitations on the number N of the Higgs doublets from the precision low-energy measurements [2]. 

... For one SM Higgs doublet, N=1, there is no unique scale μ, where {there is a unification of the Standard Model gauge couplings}. However, if at some scale μ  new states start to make additional contribution to the gauge coupling evolution, this unification point can be found... 

the physically acceptable result μ>M_Z is possible only for N≥8. Therefore, the lightest states, which can provide unification, correspond to N=8 and the scale μ=692⁺¹⁴⁴_-120 GeV... In the following only this possibility will be discussed.

... the extension of the SM with seven additional Higgs doublets looks awkward. Here we will propose a different interpretation of the given result. In [4] it was shown that the introduction of the weak-doublet spin-1 bosons V_µ=(Z^⋆_µ ,W^⋆-_µ) with the internal quantum numbers identical to the SM Higgs doublet is motivated by the hierarchy problem. It means that each spin-0 Higgs doublet is associated with the corresponding spin-1 doublet and vice versa... 

Their interactions with SU(2)_W×U(1)_Y  gauge fields are similar to the interactions of the SM Higgs doublet due to identical internal quantum numbers. The massive vector boson has three physical degrees of freedom and contributes to the gauge coupling evolution in the one-loop approximation three times more strongly than the scalar boson. Therefore, introduction of one pair of scalar and vector doublets is equivalent to the four Higgs doublets content. So, the solution with N = 8 can be interpreted as an extension of the SM Higgs sector with one additional Higgs doublet and two corresponding vector doublets. That is exactly the set of fields which was proposed in [5]. It was shown [5] that the second pair of scalar and vector doublets with opposite hypercharges is necessary to cancel the chiral anomaly.

...we concentrate here on a less-known issue connected with the production and decay of vector doublets. Interactions of vector doublets resemble scalar Higgs doublet couplings. Therefore, experimental signatures should be within the scope of those for the Higgs searches, although with obvious differences due to different spins. 

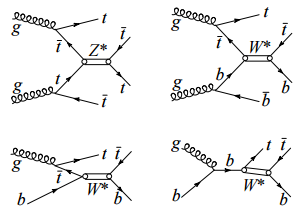
For example, the leading channel for the Higgs production at the LHC, gluon-gluon fusion through the t-quark loop, is not operative or suppressed for production of vector bosons due to the Landau–Yang theorem [12]. Vector fields cannot have nonzero vacuum expectation value unless Lorentz symmetry violation exists. Therefore, analogs of the Higgs-strahlung and weak vector boson fusion production processes are also absent for the vector doublet boson production. For the same reason the new vector boson cannot decay into two photons or two Z bosons, which are used as very clean channels for precise reconstruction of the Higgs mass. The only highly suppressed processes of heavy quark–antiquark fusion can produce resonantly the new vector bosons (Fig{ure below}).

resonant mechanism for the production of the new vector bosons

...the extension of the SM Higgs sector leads to a unification scale around 5×10¹³ GeV. This value has many specific features. For example, if the Majorana mass of a sterile right-handed neutrino is of the order of the unification scale, then the light neutrino states should have the mass of the expected order m_ν∼ v²/2μ ≈ 0.6 eV due to the see-saw mechanism [20]. Here v is the vacuum expectation value of the Higgs field. This not so high unification scale is closer to the allowed heavy Majorana neutrino masses for successful baryogenesis through leptogenesis [21]. This scale does not destroy naturality from the Planck scale [22] δm_h∼ μ³/(4π)³M²_Pl ≈0.5 GeV. On the other hand, the new lightest states at the scale μ≈700 GeV maintain naturality, solving the hierarchy problem [4]. The introduction of the spin-1 doublets with the vector degrees of freedom replaces the introduction of many scalar states with degenerate masses... 

The tb and bt¯-invariant mass distributions at √ s = 13 TeV.

...the gauge coupling unification can be achieved in the one-loop approximation by extension of the Standard Model scalar sector only with extra Higgs doublets. As a result, the unification scale is lower than other scales known in the literature and does not depend on the extra Higgs doublets, whereas a new physics scale, at which new scalar degrees of freedom become active, can be well below 1 TeV. However, this scale of new physics is reached at total number of 8 Higgs doublets, which looks very awkward. 

Therefore, we assume that spin-1 vector bosons can play the role of some of scalar degrees of freedom. In this case we get a compact fields content: two Higgs and two spin-1 doublets. However, such light states were not found in the first LHC run. The reason, as we see it, is in accepting the hypothesis of family universality of vector doublet interactions with quarks and leptons. If the vector doublet interactions resemble the Higgs fermion couplings, the new spin-1 bosons cannot be produced in light quark–antiquark annihilation from the proton beams and cannot decay into light lepton pairs as well. 

This means that the production and the decay of the new heavy bosons should be associated only with heavy band t-quarks. Moreover, the increasing gluon luminosity due to higher centre-of-mass energies in the second LHC run will lead to an order of magnitude higher cross sections for the considered processes than in the first LHC run. In conclusion, we would like to stress out that the new channel gb → tW^⋆- → tbt̅ can be very useful for early new physics search.

Signatures of lower scale gauge coupling unification in the Standard Model due to extended Higgs sector

M.V. Chizhov, V.A. Bednyakov

(Submitted on 25 Sep 2015)