The Universe also Grows ...
... but never decelerates?
The blogger would like to present here an example of a tentative to develop cosmology in the context of the noncommutative geometry model of space-time, taking advantage of the new dynamic coming from the hidden conformal longitudinal mode of the gravitational field surprisingly brought to light in the recently proposed spectral quantization of spacetime.
Quintessential Inflation models have been introduced drastically in the literature in an attempt to link inflation to the later stages of the universe’s evolution[4, 5, 6 ,7 , 8]. The key element in this unification is the fact that both inflaton, the field describing inflation, and quintessence, the field describing dark energy, are both dynamical scalar fields that are describing an accelerating expansion of the Universe...
Instead of introducing scalar fields from outside into the Lagrangian, Chamseddine and Mukhanov wrote the physical metric in the following way:
where ~gµν is an auxiliary metric, φ is (for the moment) a random scalar field and ∂α denotes partial derivative with respect to xα. In this way, one might say that the conformal mode of the metric has been isolated, for the physical metric is invariant under a conformal transformation of the auxiliary metric. It was shown in [1] that the resulting equations of motion can ”mimic” the behavior of dark matter. Therefore, one is not obliged to introduce any type of matter from outside to explain the phenomena attributed to dark matter, rather now one has to extract hidden fields from the metric to explain these phenomena...
In this chapter, we will consider a quintessential inflation model for mimetic dark matter (MDM). We start by showing from where the inspiration of the model came. We do this using the dynamics of a slow rolling field. We will then go onto considering the appropriate potential in MDM that would produce almost the same effect... the final result for the potential that would produce a quintessential inflation model in MDM is [separated... into two parts, one before inflation (t ≤ t0) and the other after inflation (t > t0)]:
while the energy density becomes:
... to determine β, we have to use the number of e-folds of inflation. If inflation is to last for 70 e-folds, then... we get: β≈7×1032... On the other hand, β' is determined by matching the value of the energy density at infinity to that of the cosmological constant [13]. This will result in β'≈√(3)×10-23 ...
These equations will result in the plots above for the scale factor and the energy density( we have used an epsilon = 0.01). From the first plot, it is clear that the scale factor is increasing with ä > 0, which implies it is an accelerated expansion of the universe. The expansion during inflation is much steeper than that after it, which is exactly what’s needed, since the universe cannot keep on accelerating at the same rate as that during inflation. Furthermore, concerning the energy density plot, the graph shows a constant energy density during inflation, which is a characteristic of inflation. In addition, the energy density reaches an asymptote as t → ∞, which is nothing but Quintessence...
In this paper... the potential used to produce [a Quintessential inflation scenario from the Mimetic Dark Matter model [1]] is defined on two time intervals, one during inflation(t = 10-36 −10-32s) and the other after inflation. The parameters of the potential were set in a way to produce 70 e-folds inflation and to have an energy density corresponding to the one measured today, representing Dark Energy. The scale factor after inflation is that of an accelerating universe, in contrast to a decelerating De-Sitter Universe as it has been presented in the literature [10]. However, in the non-modified General theory of Relativity, an energy density of matter/radiation is accompanied by a decelerating Universe, this is why usually it is required to have a decelerating universe after inflation. But in this case, from the equations of MDM, one obtains an energy density of matter/radiation dominated universe. The important thing is the energy density rather than the scale factor. Since in this model we got the required energy density but not the ”usual” scale factor, we can avoid the problem of explaining why the universe should decelerate after inflation. Rather, at the end of inflation, the universe loses enough energy for it to remain accelerating, but with a slower rate than the one during inflation. Of course we still have to check whether this will still result in the required Nucleosynthesis and we have to see if the temperature perturbations that arise matches those of the CMB. These will be handled in future work.
(Submitted on 20 Jun 2015 (v1), last revised 23 Jun 2015 (this version, v2)))
As far as the blogger can tell, Ali R. Khalifeh is a recently graduated student from American University of Beirut, Lebanon. He worked on the supervision of Ali Chamseddine.

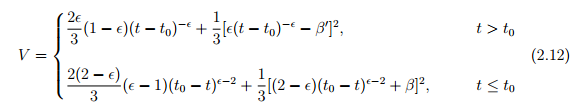




Comments
Post a Comment
Cher-ère lecteur-trice, le blogueur espère que ce billet vous a sinon interessé-e du moins interpellé-e donc, si le coeur vous en dit, osez partager avec les autres internautes comme moi vos commentaires éclairés !
Dear reader, the blogger hopes you have been interested by his post or have noticed something (ir)relevant, then if you are in the mood, do not hesitate to share with other internauts like me your enlightened opinion !