A spectral non commutative shot in the darkness of quantum physics and Einstein's gravity
Pointing to a way out of the cosmological constant problem...
Providing an Ariadne's thread to go through the dark matter and dark energy maze
Proposing a conformal extension of Einstein’s general theory of relativity
Opening a promising playground for new cosmological and astrophysical model
... in noncommutative geometry the volume of [a] compact manifold is quantized in terms of Planck units. This solves a basic difficulty of the spectral action [1] whose huge cosmological term is now quantized and no longer contributes to the field equations...
Let us study consequences of the four volume quantization for Einstein gravity... First we consider Euclidian compact spacetime and implement ... [two] kinematic constraints [associated with quantization of 4d spacetime in the spectral non commutative framework] in the action for gravity through Lagrange multipliers. This action then becomes
where 8πG=1. Notice that the last term is a four-form and represents the volume element of a unit four-sphere and can be written in differential forms as -1/(4!8)*Tr(YdY∧dY∧dY∧dY) and is independent of variation of the metric. Taking into account the [two] kinematic constraints, variation of the action with respect to the metric gives
Gµν+1/2gµνλ = 0,
where Gµν=Rµν−1/2Rgµν is the Einstein tensor. Tracing this equation gives
λ=−1/2G,
and as a result equations for the gravitational field become traceless
Gµν−1/4gµνG= 0. (15)
Using the Bianchi identity these equations imply that ∂µG=0, and hence
G=4Λ,
where Λ is the cosmological constant arising as a constant of integration...
One immediate application is that, in the path integration formulation of gravity, and in light of having only the traceless Einstein equation (15), integration over the scale factor is now replaced by a sum of the winding numbers with an appropriate weight factor. We note that for the present universe, the winding number equal to the number of Planck quanta is of the order of 1061[7].
(last revised 9 Sep 2014 (this version, v2))
Providing an Ariadne's thread to go through the dark matter and dark energy maze
... In reality spacetime is Lorentzian and generically has one noncompact dimension corresponding to time. Therefore, the condition for the volume quantization is literally non-applicable there. However being implemented in the Euclidian action it leads nevertheless to the appearance of the cosmological constant as an integration constant even in the Lorentzian spacetime... The Lorentzian action for the gravity is
[where Ya... depend on the coordinates xµ and the variable X is necessary to implement a third constraint expressed in the last term - namely the quantization of the volume of compact 3d hypersurfaces in 4d spacetime. This term] corresponds to mimetic dark matter [10],[11]. Thus the resulting action describes both dark matter and dark energy. Both substances arise automatically when the kinematic 4d and 3d compact volume quantization in noncommutative geometry is incorporated in the gravity action.
Proposing a conformal extension of Einstein’s general theory of relativity
The physical metric gphysµν is invariant with respect to the Weyl transformation of the metric gµν,
Then it was shown in [1] and in [2] that the ordinary Einstein-Hilbert action con- structed using the physical metric gphysµν possesses many interesting properties. In fact, the model analyzed below is a conformal extension of Einstein’s general theory of relativity. The local Weyl invariance is ensured by introducing an extra degree of freedom that as was shown in [1] has the form of pressureless perfect fluid that, according to [1], can mimic the behavior of a real cold dark matter.
Historically, Gunnar Nordström was the first to construct a relativistic theory of gravity as a scalar field theory [4] whose geometric reformulation [5] was the first metric theory of gravity. The physical metric of this gravitational theory was defined as a conformal transformation of the flat Minkowski metric, gµν=φ2ηµν where φ is the scalar field of Nordstr¨om’s theory. In other words, it was a theory of conformally flat spacetimes. The structure of the field equation, R=24πGT, where R and T are the traces of the Ricci tensor and the energy-momentum tensor respectively, closely resembled the field equation of the general theory of relativity formulated by Einstein in the following year. Intriguingly, the idea of mimetic matter [1] is to introduce additional fields in the conformal factor that relates the physical and auxiliary metrics (1) in such a way that the physical metric remains invariant under the conformal transformation (2).
(Submitted on 15 Apr 2014 (v1), last revised 6 Jul 2014 (this version, v3))
Opening a promising playground for new cosmological and astrophysical model
We discuss ghost free models of the recently suggested mimetic dark matter theory. This theory is shown to be a conformal extension of Einstein general relativity. Dark matter originates from gauging out its local Weyl invariance as an extra degree of freedom which describes a potential flow of the pressureless perfect fluid. For a positive energy density of this fluid the theory is free of ghost instabilities, which gives strong preference to stable configurations with a positive scalar curvature and trace of the matter stress tensor. Instabilities caused by caustics of the geodesic flow, inherent in this model, serve as a motivation for an alternative conformal extension of Einstein theory, based on the generalized Proca vector field. A potential part of this field modifies the inflationary stage in cosmology, whereas its rotational part at the post inflationary epoch might simulate rotating flows of dark matter.
(Submitted on 13 Nov 2013)
... we have extended the Mimetic Dark Matter to mimic any background cosmology. This can be achieved by adding an appropriate potential V (φ) to the original metric. As simple examples we have discussed quintessence, inflation and bouncing universe with vanishing speed of sound for perturbations.
Further, we have found another interesting novel extension which allows for the nontrivial speed of sound. This can be achieved by adding higher-order derivative terms to the action without increasing the number of degrees of freedom in the system. This allows one to quantize the inflationary scalar perturbations using standard techniques. It is demonstrated that these perturbations can have novel observational features absent in the case of k-inflation models. In particular it is possible to strongly suppress the gravitational waves from inflation, seemingly without any non-Gaussianity. It would be very interesting to analyze whether one can observationally distinguish Mimetic Inflation from other models.
Finally, such a modification opens up a new interesting playground for modeling Dark Matter, where the speed of sound can be very small but not exactly vanishing and the behavior of the mimetic matter can deviate from the usual perfect-fluid-like dust.
(Submitted on 16 Mar 2014 (v1), last revised 14 Apr 2014 (this version, v2))
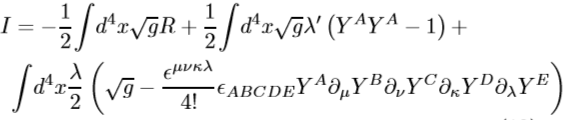




Comments
Post a Comment
Cher-ère lecteur-trice, le blogueur espère que ce billet vous a sinon interessé-e du moins interpellé-e donc, si le coeur vous en dit, osez partager avec les autres internautes comme moi vos commentaires éclairés !
Dear reader, the blogger hopes you have been interested by his post or have noticed something (ir)relevant, then if you are in the mood, do not hesitate to share with other internauts like me your enlightened opinion !