Two or three things one knows about physics in the spectral non commutative geometric paradigm

"Gravitation" can be spelled "Yang-Mills-Higgs theory" in a spectral Dirac operator language

We showed some time ago (cf. [6]) how to interpret the Lagrangian of the standard model in terms of noncommutative geometry. This interpretation was based on the extension of the Yang-Mills functional to the algebraic framework of NCG... In our joint work with A. Chamseddine [1], [2] and in [8] we showed how to incorporate the color naturally and more importantly how to obtain the bosonic part of the standard model action coupled to gravity from a very general spectral action principle. We call it a principle since it is based on the very general idea that a refined notion of geometry (suitable in particular to deal with spaces whose coordinates do not commute) is obtained by focussing not on the traditional g_µν but on the Dirac operator D... The spectral action principle then asserts that D is all that is needed to define the bosonic part of the action... 

Not surprisingly the gravitational Einstein action appears naturally in the expansion of [the spectral action], a point which is reminiscent of the idea of induced gravity. Moreover in the presence of gauge fields A the operator D gets modified (replacing derivatives by covariant derivatives) to D_A and the Yang-Mills action functional ... appears, in its Euclidean form and with the correct sign ... The simple idea developed in [1], then, is that one should understand the modification D → D_A coming from the presence of gauge fields as a slight change in the metric, while the action principle (1) which is in essence purely gravitational delivers when applied to D_A the combined Einstein-Yang-Mills action. To keep track of the “change of metric” coming from the gauge fields one needs to enhance the algebra of coordinates on the manifold M to the algebra of matrix valued functions on M which encodes the gauge group as its group of inner automorphisms.

Noncommutative Geometry and the standard model with neutrino mixing

Alain Connes, August 31st 2006

There is a non commutative geometric meaning for all the mass parameters of the Standard Model 

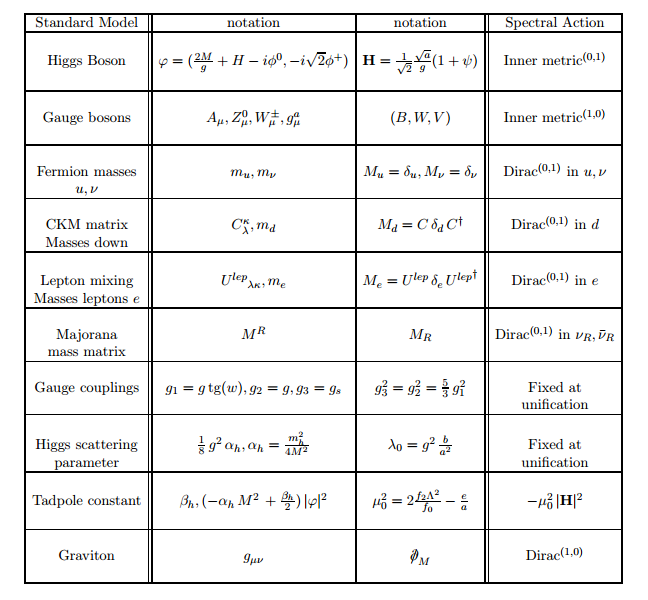
The conversion table above shows that all the mass parameters of the standard model now acquire geometric meaning as components of the noncommutative metric as displayed in the right column.

Id. 

Is fine-tuning with Majorana mass matrix terms could be how physicists Knock Out some important quantum divergence?

One needs to consider the important distinction between the following two notions of dimension of a noncommutative space:

• the metric dimension;

• The KO-dimension.

... As far as space-time goes it appears that the situation of interest will be the 4-dimensional one. In particular the metric dimension of the finite geometry F will be zero. The KO-dimension is only well defined modulo 8 ... The real surprise is that in order for things to work the only needed change (besides the easy addition of a right handed neutrino) is to change the Z/2 grading of the finite geometry F to its opposite in the “antiparticle” sector. It is only thanks to this that the Fermion doubling problem pointed out in [15] can be successfully handled. Moreover it will automatically generate the full standard model i.e. the model with neutrino mixing and the see-saw mechanism as follows from the full classification of Dirac operators...

When one looks at the table... giving the KO-dimension of the finite space F one then finds that its KO-dimension is now equal to 6 modulo 8 (!). As a result we see that the KO-dimension of the product space M × F is in fact equal to 10 ∼ 2 modulo 8. Of course the above 10 is very reminiscent of string theory, in which the finite space F might be a good candidate for an “effective” compactification at least for low energies2 . But 10 is also 2 modulo 8 which might be related to the observations of [Lauscher and  Reuter on possible Asymptotic Safety in Quantum Einstein Gravity and nonperturbative renormalizability with fractal spacetime structure]... 

The naturalness problem is of course still there, but interestingly the new terms involving [Majorana mass matrix] M_R provide room for obtaining in the spectral action a term that mimics the nasty quadratic divergence, whose coefficient changes sign under the running of the remormalization group. This freedom holds provided that the number of generations is > 1. The quadratic coupling is µ²₀=2f₂Λ²/ f₀−e/a. The presence of the new term −e/a (which was absent in [2]) allows for the possibility that the sign of this mass term is arbitrary provided there are at least two generations. We shall assume to discuss this point that the matrix M_R is ... of the form  M_R=xk_R. The value of x is fixed by the equations of motion of the spectral action i.e. by minimizing the cosmological term... Note that a similar discussion applies to the cosmological term γ₀ which inherits a negative contribution from the presence of the  M_R term.

The need to have independence between the KO-dimension and the metric dimension already emerged implicitly in the work of L. Dabrowski and A. Sitarz on Podle´s quantum spheres [10]. The results of this work were announced in a talk at the Newton Institute in July 2006... It is a pleasure to acknowledge the independent preprint by John Barrett (A Lorentzian version of the non-commutative geometry of the standard model of particle physics) with a similar solution of the fermion doubling problem.

Id.

Our geometric interpretation of the standard model gives a picture of space-time as the product of an ordinary spin manifold (in Euclidean signature) by a finite noncommutative geometry F. The geometry of F is specified by its Dirac operator D_F whose size is governed by the vacuum expectation value of the Higgs field. In other words it is the (inverse of the) size of the space F that specifies the electroweak scale. It is thus tempting to look for an explanation for the smallness of the ratio M_Z/M_Planck along the same lines as inflation as an explanation for the large size of the observable universe in Planck units.

Gravity and the standard model with neutrino mixing

Ali H. Chamseddine, Alain Connes, Matilde Marcolli, October 23rd 2006

//Last edit july 7th 2014